Одне з основних понять математичного аналізу. Неперервні функції трапляються набагато частіше, ніж диференційовні, множина всіх неперервних функцій замкнена відносноарифметичних операцій (за винятком ділення) і композиції та утворює чи не найважливіший клас функцій в аналізі. Проте строге математичне означення неперервної функції, яке належить Коші, — порівняно нещодавнє, і потребує просунутого рівня математичної абстракції. Інтуїтивне ж означення таке: функція
дійсної змінної неперервна, якщо малим змінам 
аргумента 
відповідають малі зміни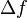 
значення функції, що можна записати так: 
коли 
Це означає, що графік неперервної функції не має стрибків, тобто може бути накреслений «не відриваючи олівець від паперу». Всі елементарні функції — неперервні на своїйобласті визначення.