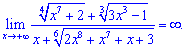ОДНОСТОРОННІ ГРАНИЦІ
Запис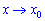 
можна розуміти, як наближення до точки 
зліва, коли 
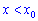і справа, коли 
. Таким чином, наближення точок 
до 
> може бути двостороннім. На основі цього введені означення правої та лівої границі.
Число 
є границею функції 
зліва (лівою границею), якщо для будь-якого числа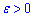 
існує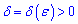 
таке, що при 
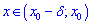виконується нерівність
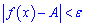
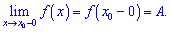
Число 
є границею функції 
справа (правою границею), якщо для як завгодно малого значення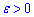 
знайдеться 
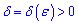таке, що для всіх 
з проміжку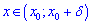 
виконується нерівність
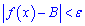
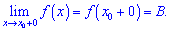
Ліва і права границі називаються одностороннніми границями.
Функція 
має границю в точці 
тоді і тільки тоді, коли існують одночасно границі справа та зліва та вони рівні між собою
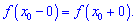
Розглянемо приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика" на знаходження границь.
-----------------------------------
Приклад 1. Знайти границі.
1) (4. 331)
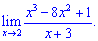
2) (4. 333)
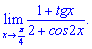
3) (4. 337)
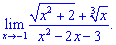
4) (4. 342)
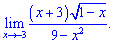
5) (4. 348)
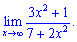
6) (4. 357)
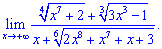
Розв'язок.
1) Перші приклади не є складними і їх розв'язування зводиться до підстановки значення аргумента у функцію
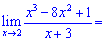
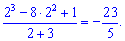
2) Як і в попередньому прикладі, проводимо підстановку
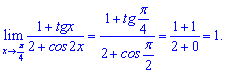
3) Виконуємо підстановку змінної
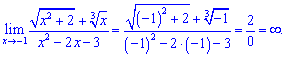
4) В такого типу прикладах потрібно знаменник розкласти за правилом різниці квадратів, після цього виконати підстановку
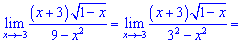
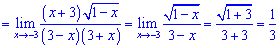
5) В таких прикладах потрібно чисельник і знаменник скоротити на множник, який вносить найбільший вклад
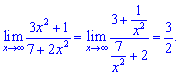
6) В подібних прикладах шукають найбільший показник змінної в
чисельнику та знаменнику, а вже потім проводять аналіз. При прямуванні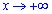 
корені поводитимуть себе наступним чином
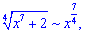
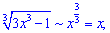
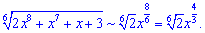
З оцінки показників бачимо, що чисельник швидше зростає ніж знаменник
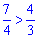
отже функція є нескінченно великою
